Introduction to Translations in Geometry

Hello!
Today, I wanted to go in to some basic geometry stuff! First, lets picture an image on a graph, like this.

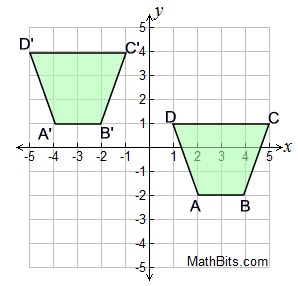
Take a look at the shape on the right. As a quick side note, when you are performing translations, the shape should never move. Think of a translation as sliding a piece of paper across a table, usually that shape stays the same direction it is. Notice how there are 4 points on the shape above (still looking at the shape on the right), A, B, C, and D? When you have to do a translation with a shape, all four of those points have to move, because the image needs to stay the same. So say I wanted you to move the shape to the left 6 points, and up 3 points. You would now have moved the shape to a different part of the graph. If you look at the left image, that would be where you moved the image to.

When you perform a translation, you should always label the points on the new image. The points should have the same letters, and they should be in the same place. One thing to note however, is when labeling the points on the new shape, you need to make them "prime". This is a fun way of saying that it is not the original shape, and that this is a new creation. See how there are little lines after the letters on the shape on the left? That is how you can tell the original image apart from the new image you have just created. You can do this for any image, not just this one!

I hope you've learned something new today!

Images From: https://mathbitsnotebook.com/Geometry/Transformations/TRTranslationsPractice.html

Equilateral, Scalene, and Isosceles Triangles, and Identifying Triangles

Hello Again!

Do you remember last time how we talked about how to tell if a triangle is right, obtuse, or acute? Remember, if it has a 90 degree angle, it is a right triangle, if it has even one angle larger than 90 degrees, then it is obtuse, and if it has all angles smaller than 90 degrees, then it is acute.

Today, I will be telling you how to identify if a triangle is Equilateral, Scalene, or Isosceles.

First, an equilateral triangle. That means that the length of all sides of the triangle is equal. They can be for any triangle, no matter how big or small, as long as all three sides are equal in length. Equilateral triangles look like this.

As a side note, when all three sides are equal, then all three angles are equal as a byproduct. Notice how there is a dash on all three sides? That is to signify that they are all the same length.

Next, an isosceles triangle is a triangle in which two of the sides are equal in length. An isosceles triangle looks like this.

Notice how there is a dash on two of the sides? That is to signify that the two sides are equal lengths.

Finally, a scalene triangle. Those are triangles that do not have the same length on any side. Each of the sides in a scalene triangle is going to be a different length, and the dashes on each side are different. Notice how there is one dash on one side, two dashes on the second side, and three dashes on the third side? That's because they are all different lengths. This is what a scalene triangle looks like.

How to Define the Angle of a Triangle

Hello!

Today I will be helping you with defining the angles of a triangle.When looking at a triangle, it can either be Right, Obtuse, or Acute.

A right triangle means there is one 90 degree angle in the triangle, that would look like this.

The square in the bottom left corner means that angle is exactly 90 degrees, which is what makes it a right triangle. A super simple way to be able to tell if it is a right triangle or not is to see if it has an "L" or not. If there is a perfect "L", then it is not right. A great visual tool to be able to tell this is if you stick one arm straight up in the air, and the other arm straight to the side.

An obtuse triangles is one that has an angle that is larger than 90 degrees. If there is even a single angle that is larger than 90 degrees, the triangle is automatically obtuse. This is what an obtuse triangle looks like.

Notice how the corner in the bottom left goes out wider than the 90 degree angle displayed above? That is what makes it obtuse. If you were to stick your arms out to make a right triangle, this shape would be wider than that.

An acute triangle is the opposite. It is when all of the angles are less than 90 degrees. That looks like this.

If you were to stick your arms out to make a right triangle, this shape would be smaller than that. That is a really simple way to identify an acute triangle.

To learn more, please go here: Acute, Obtuse and Right Triangles. I hope you all learned something from this, because my next post is going to be going off of this one!! See you next time!



Images from: Acute, Obtuse, and Right Triangles

Geometry Basics (Geometry Vocabulary for Beginners)

Hello again!

Today, I wanted to do something pretty simple. So, my next few blogs are going to be regarding geometry, so I wanted to take the time to establish some of the basics of geometry before I started going on about crazier stuff.

So, geometry is math involving shapes, as most of us know. In geometry, each part of the shapes have a name to identify them. I will be telling you the names of those shapes, as well as some basic angles.

The basic things that are in geometry are points, lines, line segments, rays, and planes

First- a point. Have you ever seen a line or a shape that has dots on each end or corner and each line is labeled A,B,C,D,E,F,G, etc? A point is the dot at the end of the lines in any given shape or line. They have those letter associated with them so that you can identify them. Here is that a simple of what points looks like.

Next, is a line. In the world of math, a line can go on forever and ever. Have you ever seen a number line? Notice how they have two dots (or more) and then arrows of either side of it? The dots represent points on the line, but the arrows mean that the line can go on forever and ever, and you can't stop it. Lines can be horizontal, vertical, diagonal, etc. Basically a line can go any direction as long as it is straight. Lines look like this.

Next, is a line segment. A line segment is a line that ends. So picture the exact same line above, except it doesn't have the arrows on the ends. That means that there is a starting point and an ending point to the line, and it doesn't go on forever. Just like a line, line segments can go any direction, as long as it is straight. Here is what a line segment looks like.

Next, there are rays. Since we already know what a line is, and what a line segment is, this will be super simple. A line segment has a starting point, but no ending point. For example, it can start at 0, and go on forever. This is what a ray looks like.

Finally, there is something called planes. Planes are a little bit harder to understand. Think of a box. You have the front, back, left side, right side, top, and bottom. each side of the box is a line segment (since it ends). The front left corner can't ever touch the back right corner, can it? No, it cannot. That is because they are on different planes. So, to put it simply, a plane is a multi-dimensional surface with different lines or line segments on it. 

If you would like to see a video of some of these things being drawn out, please go here: Line Segment, Line and Ray. If you have any questions, please let me know, and I will do my best to answer them! Next time we will talk more in depth about geometry!

Images from:

https://www.wyzant.com/resources/lessons/math/geometry/introduction/basic_geometry_terms

https://www.mathplanet.com/education/geometry/points,-lines,-planes-and-angles/an-introduction-to-geometry

Finding the Mean, Median, Mode, Range, and Outlier of a Set of Numbers

Hello Again!

Today, I will be teaching you how to find the mean, median, mode, range, and outlier of a set of numbers! First, I would like to share with you really quickly what those words mean. So mean is the same thing as the average number in a set of numbers, median is the number in the middle, and mode is the number that appears the most.

For example, say we had the numbers:

10     12     20     14     35     27     21     9     17     16     15      32     54

What are we supposed to do with those numbers? Well, usually I would start with putting them in order, because my OCD would go crazy otherwise. Also, putting the numbers in order is required to help us find some of the information we need a little bit later. So this is what those numbers would look like in order:

9     10     12     14     15     16     17     20     21     27     32      35     54

That's better! Now then, first lets get the hardest thing out of the way- the mean. Some would say that it is called the mean because it is the hardest one to find. The way you find the mean (or average) is by adding all of numbers together, and then dividing the total that you get by how many numbers there are. So, 9 + 10 + 12 + 14 + 15+ 16 + 17 + 20 + 27 + 32 + 35 + 54 = 261. Now, we count how many numbers there are, and we know that there are 12 numbers. So now we take that 261 total that we got, and divide it by 12. So 261 ፥ 12= 21.75. That means that our mean for the whole set of numbers is 21.75.

Next, we are going to find the median. This is a very simple thing to do. This is where you would have needed to put the numbers in order, if you haven't already. The easiest way to find the median is to cross out numbers on either side until you reach the middle, like this:

9     10     12     14     15     16     17     20     21     27     32      35     54

9     10     12     14     15     16     17     20     21     27     32      35     54

9     10     12     14     15     16     17     20     21     27     32      35     54

9     10     12     14     15     16     17     20     21     27     32      35     54

9     10     12     14     15     16     17     20     21     27     32      35     54

9     10     12     14     15     16     17     20     21     27     32      35     54

After crossing out all of the numbers, we can see that 17 is the number in the middle, or the median. Easy right? In this case, we had an odd amount of numbers, so our median was only one number, but if you had an even amount of numbers you would have two numbers that you didn't cross out. In that case, you would just add the two numbers together and divide by 2. That would then be your median!

On to the mode! This is probably the easiest of them all! Since I told you earlier that mode means the number that appears the most, you would just look for the number that shows up the most amount of times. However, in our case, each number only appears once, so there is no mode. There can be situations where there is more than one mode though, when there is more than one number that appears the same amount of times. 

Next there is the range. This is another simple one. All you do in this case is subtract the highest number and the lowest number. The highest number is 54, and the lowest number is 9, so we would do 54 - 9 which equals 45. That means 45 is the range!

Finally, on to the outlier. The outlier is that one number that is way off from the rest of them. In this case, all of these numbers are pretty close to each other, except for 54. That would mean that 54 is our outlier. An outlier is important in situations where maybe there is a class of test scores, and someone scores much lower or much higher than the rest of the class. That number that is way off would affect the mean, so usually you wouldn't include it just so the numbers stay more fair.

If you would like to know more, please visit this website! Mean, Median, Mode and Range

I hope my explanations were thorough enough! Please leave me a comment if you have any questions. Until next time!

The Basics of Probability

Probability

Hello Everybody! Today I wanted to do a short lesson on Probability. 

How many times in your life have you played a dice game, and you had to roll number three in order to win. So you're shaking the dice in your hands, and your saying to yourself "come on...come on...." and then you throw that dice. Do you really know what your chances are of getting that number? This is what I am here to tell you today!

Okay, so first things first, probability is always written as a fraction. There is actually a formula to determine the probability of something happening. If you would like to know what that formula is, click here: Probability Formula

However, for someone who is new to learning anything about probability, that is really confusing. The way that I choose to think of it is how many ways you can get what you are looking for over how many ways there are total. So, in our case, we are only looking for one specific number (the number that we are looking for is 3, and there is only one 3 in a single dice) over a total of 6 numbers. That means that our probability of rolling a 3 is: 1/6.

Say you wanted to get any even number instead of just the number 3. Then you know that there is 3 even numbers on a dice, and 6 total numbers, that would make your answer 3/6. However, in this case you would need to simplify because 3/6 is the same thing as saying 1/2. That would mean the probability of rolling an even number is 1/2.

This same method can be done to determine lots of different things. For example, if you are flipping a coin and you want it to land on heads, you know that there is 1 outcome that you want over 2 total potential outcomes. That would mean that your probability of landing a heads on a coin toss is 1/2.

Please let me know if you have any questions about the basics of probability!